8주차(최소신장트리) - [C++]백준2887 행성 터널

11 May 2022 in Study on Algorithm

백준2887 행성 터널 링크

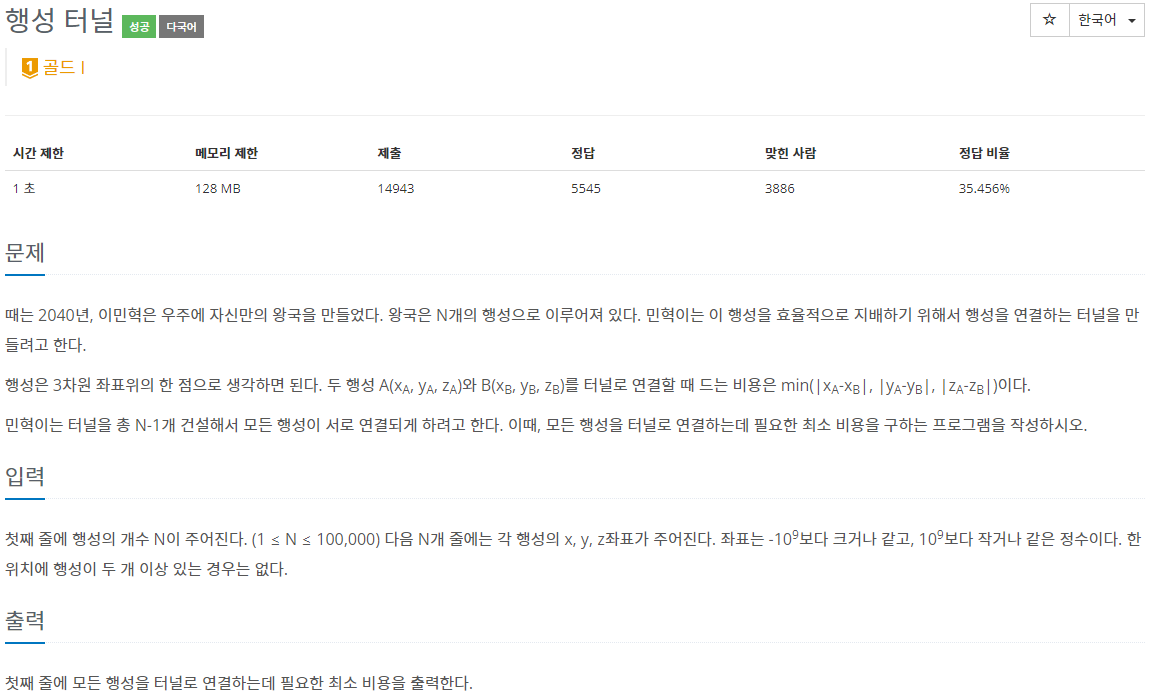
문제

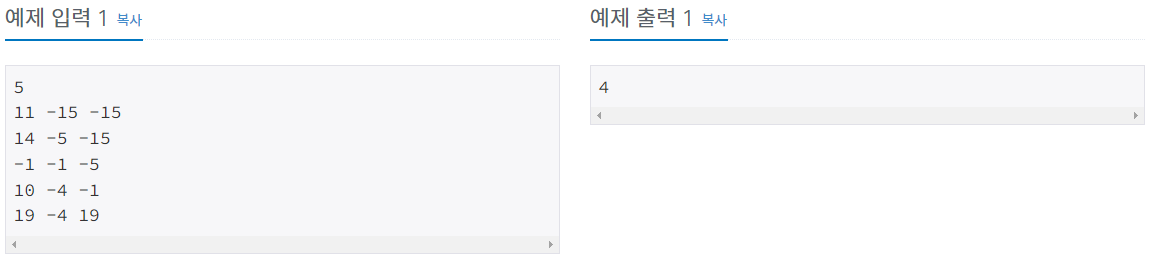
예제 입력

---

코드

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

int arr[100001];
vector<pair<int, int>> dx;
vector<pair<int, int>> dy;
vector<pair<int, int>> dz;
vector<pair<int, pair<int, int>>> vec;

// 원소가 속한 집합 찾기  
int find(int x) {
    if (arr[x] != x) arr[x] = find(arr[x]);
    return arr[x];
}

// 두 원소 집합 합치기  
void Union(int a, int b) {
    a = find(a);
    b = find(b);
    if (a < b) arr[b] = a;
    else arr[a] = b;
}

int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) arr[i] = i;

    // 정점 좌표 + 번호
    for (int i = 1; i <= n; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        dx.push_back({ a, i });
        dy.push_back({ b, i });
        dz.push_back({ c, i });
    }
    sort(dx.begin(), dx.end());
    sort(dy.begin(), dy.end());
    sort(dz.begin(), dz.end());

    // 간선 만들기
    for (int i = 0; i < n - 1; i++) {
        vec.push_back({ dx[i + 1].first - dx[i].first, {dx[i].second, dx[i + 1].second} });
        vec.push_back({ dy[i + 1].first - dy[i].first, {dy[i].second, dy[i + 1].second} });
        vec.push_back({ dz[i + 1].first - dz[i].first, {dz[i].second, dz[i + 1].second} });
    }
    sort(vec.begin(), vec.end());

    // 크루스칼 알고리즘
    int cost = 0;
    for (int i = 0; i < vec.size(); i++) {
        if (find(vec[i].second.first) != find(vec[i].second.second)) {
            Union(vec[i].second.first, vec[i].second.second);
            cost += vec[i].first;
        }
    }
    cout << cost;
}

설명

이 문제는 3차원상에 행성들의 위치에서 다른 행성으로 터널을 연결할때 어느 한 좌표라도 드는 비용이 최소인 것을 선택하여 모든 행성을 효율적으로 연결하는 것입니다. C++ STL(표준 템플릿 라이브러리)에서 vector를 사용하여 구현했습니다. 행성들의 위치 정보를 입력 받아 MST로 최소 비용을 구해야하는데 다른 문제들과 다르게 1개의 행성마다 갈 수 있는 간선이 3가지로 바뀐 것입니다. 그래서 각각 x, y, z로 저장하고 그다음에 1차원으로 값을 생각하니 정렬하여 순서를 크기순으로 맞추었습니다. 그리고 간선을 만들때는 두 수를 빼서 각각 x, y, z로 직접 만들어 줬습니다. 그 상태에서 크루스칼 알고리즘을 사용하기 위해서 간선을 오름차순으로 정렬하고 최소신장트리의 결과를 구하였습니다.

-pair<자료형, 자료형> 변수명; : 하나의 변수에 2가지 값을 저장함

<algorithm>
-sort(시작, 끝, 비교함수) : 배열의 크기만큼 정렬

<vector>
-vector<자료형> 변수명; : 배열 자료구조 사용

---

결과