7주차(최단경로) - [C++]백준1504 특정한 최단 경로

30 Apr 2022 in Study on Algorithm

백준1504 특정한 최단 경로 링크

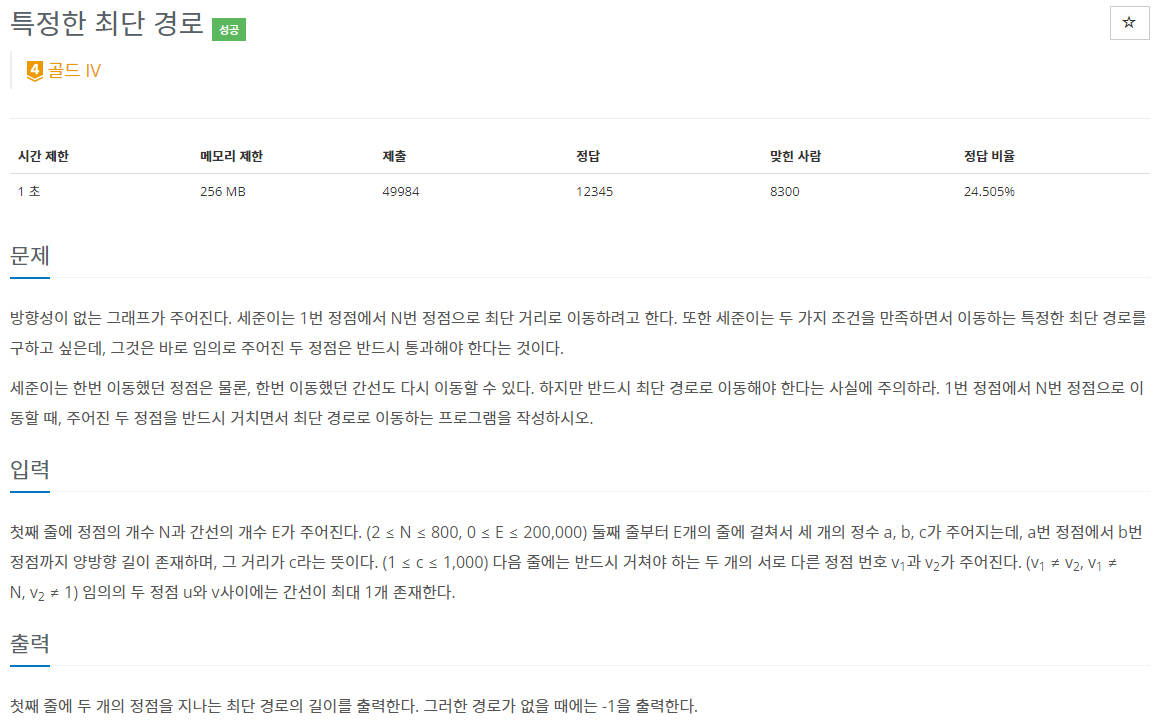
문제

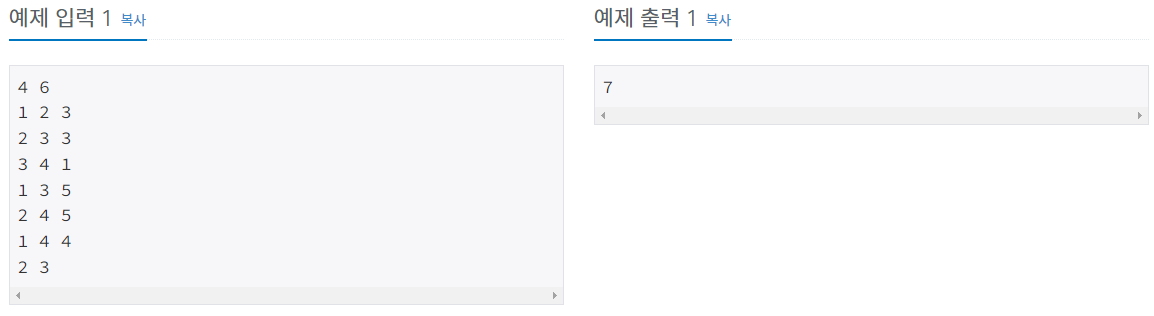
예제 입력

---

코드

#include<iostream>
#include<vector>
#include<queue>
#define INF 1e9
using namespace std;

int n, e;
vector<pair<int, int>> Graph[801];
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
int Dist[801];

void dijkstra(int start) {
	fill(Dist, Dist + n + 1, INF);
    Dist[start] = 0;
	//첫 번째 길이, 두 번째 정점
	pq.push({ Dist[start],start });

    while (!pq.empty()) {
        auto cur = pq.top();
        pq.pop();
        if (Dist[cur.second] < cur.first) continue;
        for (auto nxt : Graph[cur.second]) {
            if (Dist[nxt.first] > Dist[cur.second] + nxt.second) {
                Dist[nxt.first] = Dist[cur.second] + nxt.second;
                pq.push({ Dist[nxt.first], nxt.first });
            }
        }
    }
}

int main() {
	ios_base::sync_with_stdio(0);
    cin.tie(0); //cin 실행속도 향상

    cin >> n >> e;
    for (int i = 0; i < e; i++) {
        int from, to, dist;
        cin >> from >> to >> dist;
        Graph[from].push_back({ to, dist});
        Graph[to].push_back({ from, dist});

    }

    int v1, v2;
    cin >> v1 >> v2;

    dijkstra(1); //1 ->v1 또는 1->v2 
    int d1_v1 = Dist[v1];
    int d1_v2 = Dist[v2];

    dijkstra(v1); //v1 -> v2 또는 v1 -> N
    int dv1_v2 = Dist[v2];
    int dv1_n = Dist[n];

    dijkstra(v2); //v2 -> v1 또는 v2 -> N
    int dv2_n = Dist[n];
    int dv2_v1 = Dist[v1];

    int sum1 = d1_v1 + dv1_v2 + dv2_n;
    int sum2 = d1_v2 + dv2_v1 + dv1_n;

    int ans = min(sum1, sum2);
    if (ans >= INF) cout << -1;
    else cout << ans;
}

설명

이 문제는 시작점을 1로하고 나머지 특정한 두 점을 지나 종료점까지의 거리중 최단 경로를 구하는 것입니다. C++ STL(표준 템플릿 라이브러리)에서 vector와 Queue를 사용하여 구현했습니다. 무방향 그래프이기 때문에 양쪽에 같은 거리를 입력 받아 1부터 v1, v2를 지나 n까지의 최단 경로를 찾기 위해서 다익스트라 알고리즘을 사용하는데 시작점으로부터 종료점이나 다른 정점과 찾는 특성상 한 번에 찾지 못하기 때문에 차례대로 각각의 경로인 1->v1->v2->n와 1->v2->v1->n를 3번에 걸쳐서 구했습니다. 최소 힙을 사용하여 각 정점으로 가는 경로에 대한 값을 Dist에 넣어주고 이미 있다면 비교하여 최단 경로로 갱신 해줍니다. 확인할때는 둘다 경로가 없다면 -1을 출력하고 하나 이상있다면 그들중 최단 거리를 출력합니다.

-pair<자료형, 자료형> 변수명; : 하나의 변수에 2가지 값을 저장함

<vector>
-vector<자료형> 변수명; : 배열 자료구조 사용

<queue>
-priority_queue<자료형, 자료형태, 비교함수> 변수명; : 우선순위 큐(힙) 자료구조 사용
<비교함수>
-greater<자료형> : 내림차순 정렬
-less<자료형> : 오름차순 정렬

---

결과