[Python] 백준1389 케빈 베이컨의 6단계 법칙

20 Jan 2023 in Study on Algorithm

백준1389 케빈 베이컨의 6단계 법칙 링크

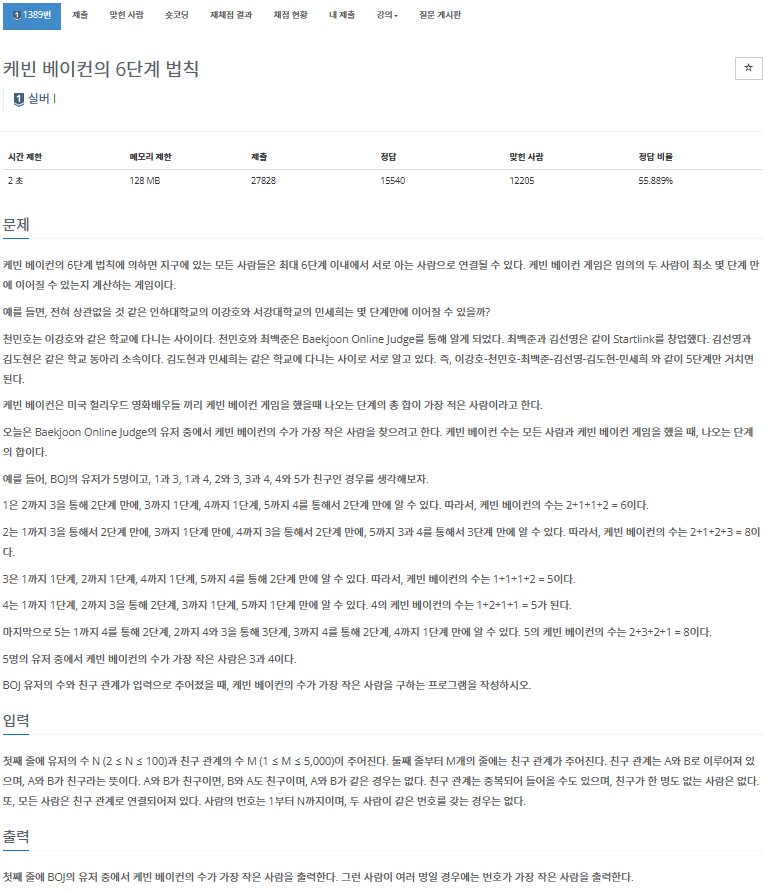
문제

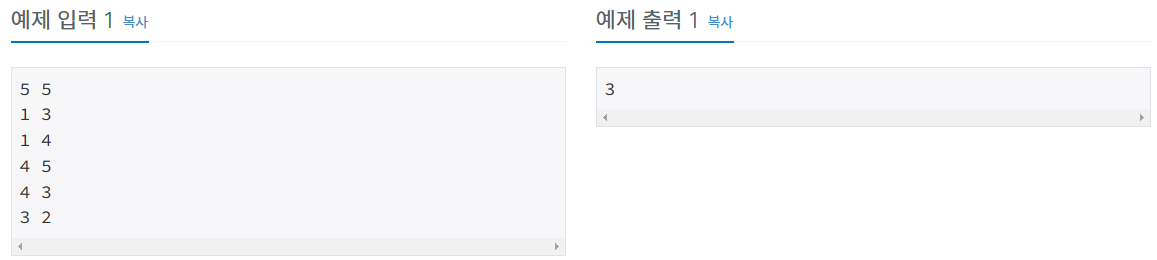
예제 입력

---

코드

import sys
import math

n, m = map(int, input().split())
arr = [ [ math.inf ] * n for _ in range(n) ]

for _ in range(m):
    a, b = map(int, sys.stdin.readline().split())
    arr[a - 1][b - 1] = 1
    arr[b - 1][a - 1] = 1

# 플로이드 워셜 알고리즘
for k in range(n):
    for i in range(n):
        for j in range(n):
            if i == j:
                arr[i][j] = 0
            else :
                arr[i][j] = min(arr[i][j], arr[i][k] + arr[k][j])

res = []
for row in arr:
    res.append(sum(row))
print(res.index(min(res)) + 1)

설명

파이썬을 통해서 사용자로부터 입력받아 자료형 list를 사용하여 플로이드 워셜 알고리즘으로 케빈 베이컨의 6단계 법칙를 구현했습니다.

---

정리

ans = 0
min = float("inf")
for i in range(n):
    sum = 0
    for j in range(n):
       arr[i][j] = 0
    if min > sum:
        min = sum
        ans = i + 1
print(ans)

math의 무한대 외에도 float를 사용한 무한대로 결과를 구할 수 있습니다.

플로이드 워셜 - 모든 노드에서 다른 모든 노드까지의 최단 경로를 모두 계산 (O(N^3))

다익스트라 알고리즘 - 매 상황에서 방문하지 않은 가장 비용이 적은 노드를 선택(한 단계당 하나의 노드에 대한 최단 거리를 확실히 찾는 것), 시간을 줄이기 위해서 우선순위 큐 활용 (O(NlogN))

---

결과