[Python] 백준1865 웜홀

25 Jun 2023 in Study on Algorithm

백준1865 웜홀 링크

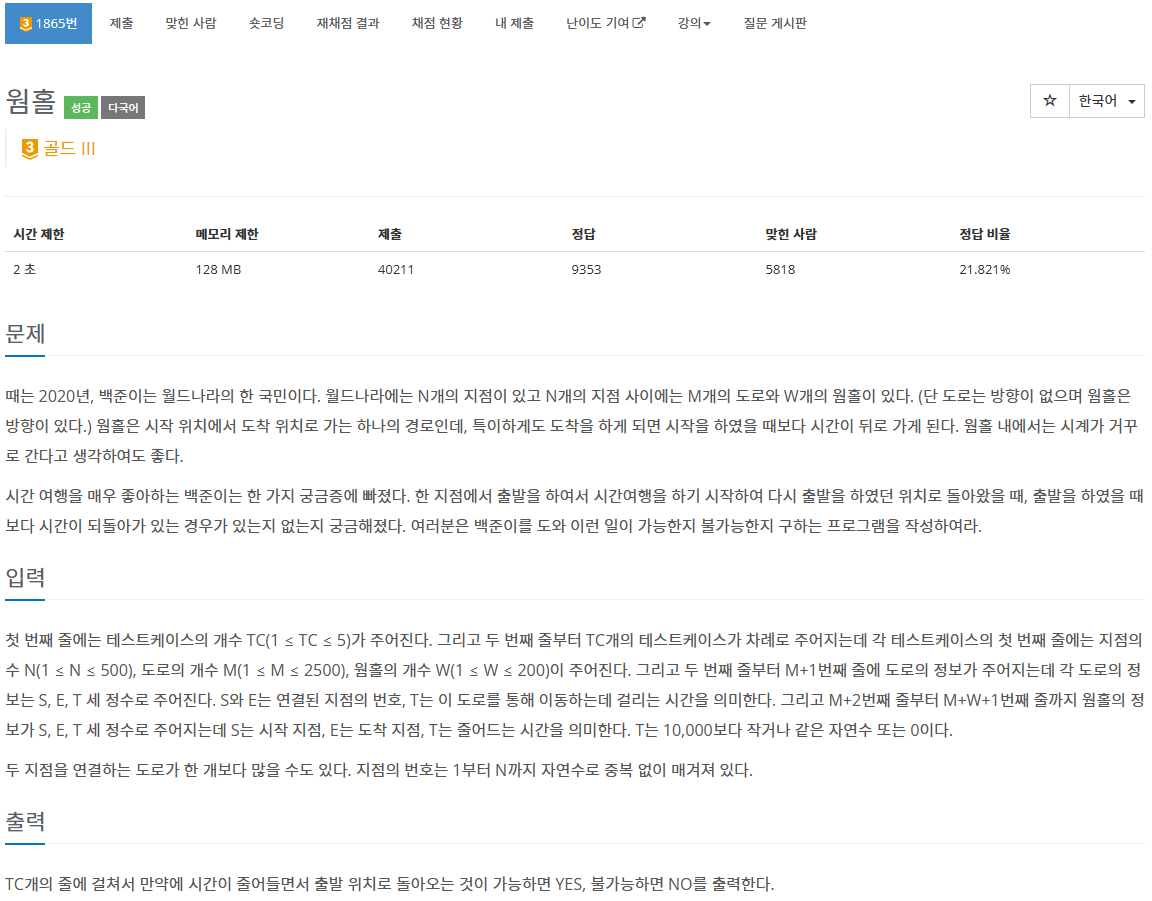
문제

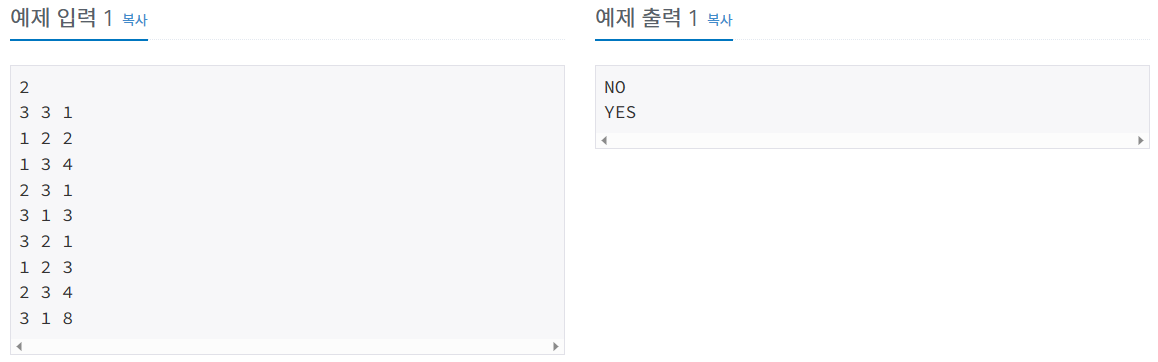
예제 입력

---

코드

import sys
# float("inf")사용하면 무한대 + 음수일때 문제 발생.
INF = 2147483647

# 벨만-포드
def bf(start):
    dist[start] = 0

    # 정점 개수(N-1)만큼 반복 = 매번 모든 간선을 확인.
    for k in range(1, N+1):
        for i in range(1, N+1):
            for pos, val in arr[i]:
                if dist[pos] > dist[i] + val:
                    dist[pos] = dist[i] + val

                    # N번째에도 된다면 음수 사이클 => N-1의 간선만 해도 최적.
                    if k == N:
                        print("YES")
                        return
    print("NO")
    return 

TC = int(input())
for _ in  range(TC):
    N, M, W = map(int, sys.stdin.readline().split())
    
    arr = [[] for _ in range(N+1)]
    dist = [INF] * (N+1)

    for _ in range(M):
        S, E, T = map(int, sys.stdin.readline().split())
        arr[S].append([E, T])
        arr[E].append([S, T])

    for _ in range(W):
        S, E, T = map(int, sys.stdin.readline().split())
        arr[S].append([E, -T])
    
    bf(1)

# 벨만-포드 알고리즘
# 다익스트라 알고리즘(그리디)처럼 가중치 있는 그래프에서 어떤 출발점으로 부터의 최단경로를 찾는 단일 시작점 최단경로 알고리즘입니다. 
# 단, 다익스트라 알고리즘에서는 그래프에 음수 간선의 순환(-무한대)이 포함되어 있을경우 쓸 수 없다는 단점이 있었는데 벨만포드는 그러한 음수간선이 있을 경우에도 작동하는 알고리즘이라 할 수 있습니다.
# 이처럼 벨만포드 알고리즘은 기능만 보면 다익스트라 알고리즘의 상위호환인 알고리즘이지만 시간복잡도 측면에서는 다익스트라보다 조금 뒤쳐지기 때문에 상황에 맞는 알고리즘을 선택하는 것이 좋을 것이다.
# 1. 음수 가중치가 있는 그래프의 시작 정점에서 다른 정점까지의 최단 거리를 구할 수 있습니다.
# 2. 음수 사이클 존재의 여부를 알 수 있습니다.

설명

파이썬을 통해서 사용자로부터 입력받아 벨만-포드 알고리즘을 사용하여 웜홀를 구현했습니다.

---

결과