7주차(최단경로) - [C++]백준4485 녹색 옷 입은 애가 젤다지?

02 May 2022 in Study on Algorithm

백준4485 녹색 옷 입은 애가 젤다지? 링크

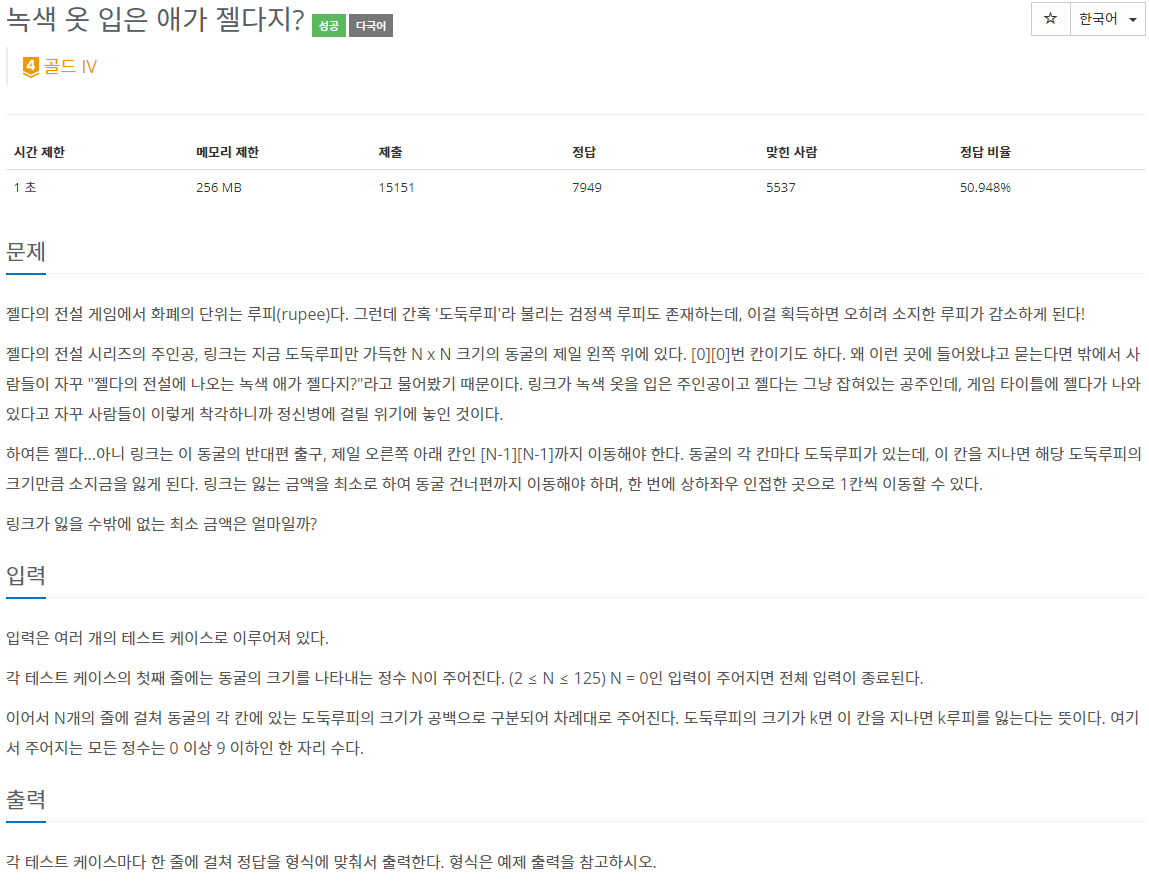
문제

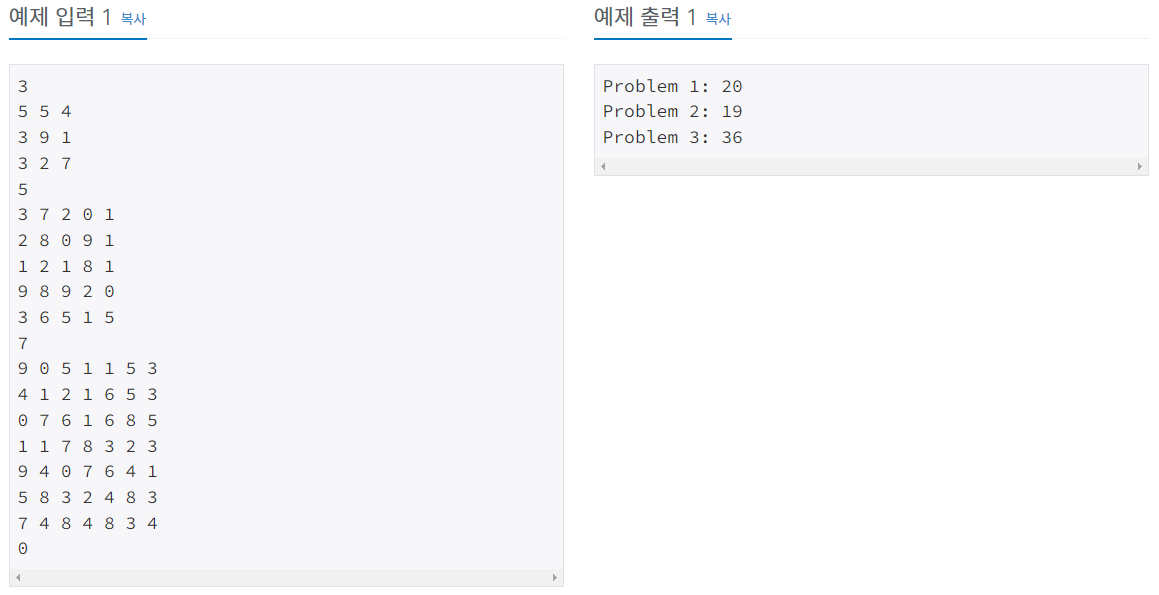
예제 입력

---

코드

#include<iostream>
#include<queue>
#define INF 1e9
using namespace std;

int n, cnt = 0;
priority_queue<pair<int, pair<int, int>>, vector<pair<int, pair<int, int>>>, greater<pair<int, pair<int, int>>>> pq;
int Dist[125][125];
int arr[125][125];

int dx[] = { 0, 0, 1, -1 };
int dy[] = { 1, -1, 0, 0 };

void dijkstra() {
    Dist[0][0] = arr[0][0];
    pq.push({ Dist[0][0], {0, 0} });

    while (!pq.empty()) {
        int dist = pq.top().first;
        int cx = pq.top().second.first;
        int cy = pq.top().second.second;
        pq.pop();

        for (int i = 0; i < 4; i++) {
            int nx = cx + dx[i];
            int ny = cy + dy[i];

            if (0 <= nx && nx < n && 0 <= ny && ny < n) {
                int ndist = dist + arr[nx][ny];
                if (ndist < Dist[nx][ny]) {
                    Dist[nx][ny] = ndist;
                    pq.push({ ndist, {nx, ny} });
                }
            }
        }
    }
}

int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0); //cin 실행속도 향상

    while (true) {
        cin >> n;
        if (n == 0) break; 
        // 입력  
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                cin >> arr[i][j];
                Dist[i][j] = INF;  
            }
        }
        dijkstra(); 

        int ans = Dist[n - 1][n - 1];
        cout << "Problem " << ++cnt << ": " << ans << '\n';
    }
}

설명

이 문제는 동굴에 시작 지점에서 종료 지점까지 빠져나오는데 각 칸마다 루피를 잃는 리스크가 있어서 어느 경로로 가야 최소의 리스크로 빠져나오는지에 대한 최단 경로를 구하는 것입니다. C++ STL(표준 템플릿 라이브러리)에서 vector와 Queue를 사용하여 구현했습니다. 사실상 문제에 대한 조건들은 보고 BFS로 풀기 좋다고 생각했지만 분류상 다익스트라(데이크스트라)로 되어 있어 이 방향으로 풀게 되었습니다. 먼저 동굴에 대한 정보를 입력 받아 각 동굴의 위치를 하나의 정점으로 생각하고 상, 하, 좌, 우에 경로가 있다고 생각했습니다. 이제 최단 경로를 찾기 위해서 다익스트라 알고리즘을 사용하는데 고정된 시작점으로부터 고정된 종료점까지 최단 경로를 찾습니다. 최소 힙을 사용하여 각 정점으로 가는 경로에 대한 값과 현재 값을 더한 후 Dist에 넣어주고 이미 있다면 비교하여 최단 경로로 갱신 해줍니다. 마지막으로 종료 지점의 값이 여태까지 모든 경로를 탐색하고 나온 최소의 리스크이며 최단 경로라서 출력합니다.

-pair<자료형, 자료형> 변수명; : 하나의 변수에 2가지 값을 저장함

<queue>
-priority_queue<자료형, 자료형태, 비교함수> 변수명; : 우선순위 큐(힙) 자료구조 사용
<비교함수>
-greater<자료형> : 내림차순 정렬
-less<자료형> : 오름차순 정렬

---

결과